Hojas de Ejercicios de Geometría

¡Bienvenido a la página de hojas de ejercicios de geometría de MatesLibres.com, donde creemos que no hay nada de malo en ser un cuadrado!

¡Saquen sus reglas, semicírculos y compases, porque tenemos algunas hojas de ejercicios de geometría geniales! Los cuadriláteros se pueden cortar, medir, doblar, comparar e incluso se les puede escribir encima. Pueden ser muy útiles a la hora de enseñar todo tipo de conceptos relacionados con los cuadriláteros. Justo debajo de ellos, encontrará hojas de ejercicios sobre geometría de ángulos. Vea también la página de medidas para más hojas de ejercicios sobre ángulos.La mayor parte de la página está dedicada a las transformaciones. La geometría de transformaciones es uno de esos temas que puede ser interesante para los estudiantes y tenemos preparadas suficientes hojas de ejercicios sobre este tema de geometría como para tener a los alumnos ocupados durante horas.

No se pierda el mundo complejo pero interesante de los cubos conectados, al final de la página. Puede que encuentre algunos futuros artistas cuando emplee estas hojas de ejercicios con sus alumnos.

Hojas de Ejercicios de Geometría más populares esta semana

Formas Básicas

Tangrams

El set de cuadriláteros puede ser usado para un número de actividades que incluyen clasificar y reconocer cuadriláteros o para investigar las propiedades de los cuadriláteros (p.ej. que la suma de los ángulos interiores es 360 grados). Los tangrams imprimibles son útiles para actividades con tangrams. Hay varias opciones para los tangrams imprimibles dependiendo de su impresora, y cada opción incluye una versión grande y una más pequeña. Si conoce a alguien que tenga una sierra adecuada, puede usar los tangrams imprimibles como plantillas para hacer piezas de un material como madera contrachapada; luego simplemente lije y pinte las piezas.

Tangrams

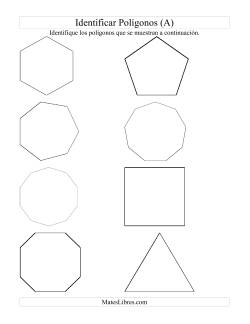
Identificar Formas

Identificar Polígonos Regulares

Hojas de Ejercicios de Geometría de ángulos

Ejercicios de geometría con ángulos, para identificar ángulos y relaciones entre ángulos.

Qué sería una página de geometría sin hojas de ejercicios de ángulos. Hemos tratado de enfocarnos en esta sección en nombrar ángulos y en las relaciones de ángulos. Si lo que busca son ejercicios de medir ángulos, por favor visite nuestra Página de Medidas

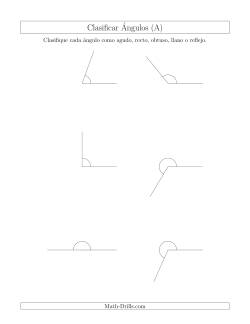
Clasificar ángulos

Clasificar ángulos Simples Clasificar Todo Tipo de ángulos

Relaciones Entre ángulos

ángulos Complementarios ángulos Suplementarios ángulos Opuestos por el Vértice ángulos Alternos Interiores ángulos Alternos Exteriores ángulos Alternos ángulos Correspondientes ángulos Conjugados Interiores Todos los ángulos Entre Paralelas

Geometría de Puntos Coordenados

El "punto" de las hojas de ejercicios de esta sección es ayudar a los estudiantes a aprender acerca del plano cartesiano. Hemos creado unas cuantas hojas de ejercicios únicas a continuación para ayudar a los alumnos con sus estudios.

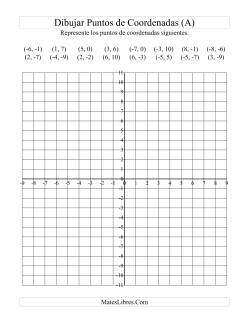
Representar Puntos de Coordenadas

Representar Puntos en Todos los Cuadrantes Representar Puntos en los Cuadrantes con x Positiva Representar Puntos en los Cuadrantes con y Positiva

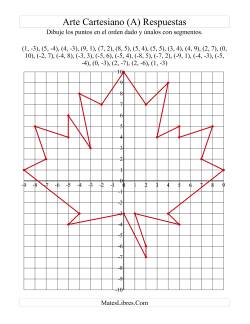
Arte Cartesiano por MatesLibres.com

Hoja de Arce

Distancias y áreas en el Plano Cartesiano

Calcular la Distancia Pitagórica Entre Dos Puntos Calcular el Perímetro y el área de Triángulos Calcular el Perímetro y el área de Cuadriláteros Calcular el Perímetro y el área de Triángulos y Cuadriláteros

Triángulos

Hojas de ejercicios para clasificar triángulos de acuerdo a sus lados y ángulos.

Para mayor información sobre cómo clasificar triángulos, vea nuestra Guía sobre los diferentes tipos de triángulos, así como nuestra Hoja de referencia rápida sobre el mismo tema.

Clasificar Triángulos

Clasificar Triángulos de Acuerdo a sus Lados Clasificar Triángulos de Acuerdo a sus ángulos

Cuadriláteros

Hojas de ejercicios para clasificar cuadriláteros.

Clasificar Cuadriláteros

Clasificar Cuadriláteros Simples Clasificar Todo Tipo de Cuadriláteros Clasificar Todo Tipo de Cuadriláteros (incluyendo rotaciones)

Ejercicios de Transformaciones

Hojas de ejercicios de traslaciones, reflexiones, rotaciones y homotecias.

Las siguientes son dos maneras fáciles de comprobar las respuestas de sus alumnos en las hojas de ejercicios de geometría de transformaciones que aparecen a continuación. Primero, puede alinear la hoja del estudiante con la hoja de respuestas, y mirarlas a trasluz. Al mover o deslizar las páginas ligeramente, podrá comprobar si las respuestas del alumno son correctas. Mantenga la página del estudiante encima y márquela o hágale recomendaciones según sea necesario. El segundo método es fotocopiar la hoja de respuestas en una transparencia. Coloque la transparencia sobre la hoja del estudiante, y levántela cuando sea necesario hacer marcas o sugerencias.

Traslaciones Simples

Traslación de 3 vertices por hasta 3 unidades Traslación de 3 vertices por hasta 6 unidades Traslación de 3 vertices por hasta 25 unidades Traslación de 4 vertices por hasta 6 unidades Traslación de 5 vertices por hasta 6 unidades

Traslaciones Compuestas

Traslación en Dos Pasos de 3 vertices por hasta 6 unidades Traslación en Dos Pasos de 4 vertices por hasta 6 unidades Traslación en Tres Pasos de 3 vertices por hasta 6 unidades Traslación en Tres Pasos de 4 vertices por hasta 6 unidades

Reflexiones sobre esto: reflejar formas a través de líneas verticales u horizontales es bastante sencillo, sobre todo si hay una cuadrícula involucrada. Comience en uno de los puntos/vértices originales y mida la distancia hasta ala línea de reflexión. Note que debe medir perpendicularmente o 90 grados hacia la línea, razón por la cual es más sencillo con líneas de reflexión verticales u horizontales que con líneas diagonales. Mida 90 grados en el otro lado de la línea de reflexión, además de la misma distancia por supuesto, y dibuje un punto para representar el vértice reflejado. Una vez que haya hecho esto con todos los vértices, simplemente dibuje los segmentos de lía y su forma reflejada estará completa.

Reflejar puede también ser tan simple como doblar un papel. Doble la hoja a lo largo de la línea de reflexión y mire el papel a trasluz. Es mejor hacerlo en una ventana, porque sirve además de superficie de apoyo. Sólo marque los vértices, no trate de dibujar la forma entera. Desdoble el papel y use lápiz y regla para dibujar los segmentos de línea entre los vértices.

Reflexiones Simples

Reflexión de 3 Vértices Sobre x = 0 y y = 0 Reflexión de 4 Vértices Sobre x = 0 y y = 0 Reflexión de 5 Vértices Sobre x = 0 y y = 0 Reflexión de 3 Vértices Sobre Varios Ejes Reflexión de 4 Vértices Sobre Varios Ejes Reflexión de 5 Vértices Sobre Varios Ejes

Reflexiones Compuestas

Reflexión en Dos Pasos de 3 Vértices Sobre Varios Ejes Reflexión en Dos Pasos de 4 Vértices Sobre Varios Ejes Reflexión en Tres Pasos de 3 Vértices Sobre Varios Ejes Reflexión en Tres Pasos de 4 Vértices Sobre Varios Ejes

Aquí les damos una idea de cómo completar rotaciones sin necesidad de medir. Funciona mejor en una cuadrícula, y con rotaciones de 90 ó 180 grados. Necesitará una hoja de transparencias en blanco o alguna otra hoja adecuada de plástico transparente, y una pluma que pueda escribir sobre esa hoja. Las plumas de tinta no permanente son mejores porque así se podrá lavar y reutilizar la hoja. Coloque la hoja sobre los ejes de coordenadas con la figura que se va a rotar. Con la pluma, haga una peque˜a cruz para indicar los ejes x e y tan claro como sea posible. También marque los V6eacute;rtices de la figura que va a ser rotada. Usando la hoja de plástico, realice la rotación, alineando la cruz de nuevo con los ejes. Elija un vértice y márquelo en el papel sosteniendo la hoja plástica en su sitio, pero levantándola lo suficiente como para poder hacer una marca. Haga lo mismo con los otros vértices, y luego retire la hoja plástica y una los vértices consegmentos de línea usando una regla.

Rotaciones Simples

Rotación de 3 Vértices Alrededor del Origen Comenzando en el Cuadrante I Rotación de 4 Vértices Alrededor del Origen Comenzando en el Cuadrante I Rotación de 5 Vértices Alrededor del Origen Comenzando en el Cuadrante I Rotación de 3 Vértices Alrededor del Origen Rotación de 4 Vértices Alrededor del Origen Rotación de 5 Vértices Alrededor del Origen Rotación de 3 Vértices Alrededor de Cualquier Punto Rotación de 4 Vértices Alrededor de Cualquier Punto Rotación de 5 Vértices Alrededor de Cualquier Punto

Rotaciones Compuestas

Rotaciones en Dos Pasos de 3 Vértices Alrededor de Cualquier Punto Rotaciones en Dos Pasos de 4 Vértices Alrededor de Cualquier Punto Rotaciones en Dos Pasos de 5 Vértices Alrededor de Cualquier Punto Rotaciones en Tres Pasos de 3 Vértices Alrededor de Cualquier Punto Rotaciones en Tres Pasos de 4 Vértices Alrededor de Cualquier Punto Rotaciones en Tres Pasos de 5 Vértices Alrededor de Cualquier Punto

Homotecia y Escalas

Homotecias Usando el Centro de Coordenadas (0, 0) Homotecias Usando Centros Variados Determinar el Factor de Escala de Rectángulos, con Valores Enteros Determinar el Factor de Escala de Rectángulos, con Intervalos de 0,5 Determinar el Factor de Escala de Rectángulos, con Valores de 0,1 Determinar el Factor de Escala de Triángulos, con Valores Enteros Determinar el Factor de Escala de Triángulos, con Intervalos de 0,5 Determinar el Factor de Escala de Triángulos, con Valores de 0,1 Determinar el Factor de Escala de Figuras Diversas, con Valores Enteros Determinar el Factor de Escala de Figuras Diversas, con Intervalos de 0,5 Determinar el Factor de Escala de Figuras Diversas, con Valores de 0,1

Transformaciones Geométricas Combinadas

Dos Pasos de Transformaciones Tres Pasos de Transformaciones

Ejercicios de Construcciones

Ejercicios de contrucciones para aprender a dibujar bisectrices, rectas perpendiculares y centros de triángulos.

Es increíble lo que se puede lograr con un compás, una regla y un lápiz. En esta sección, los estudiantes harán matemáticas como mismo lo hizo Euclides, hace más de 2000 años. No sólo será una lección de historia, sino que sus estudiantes podrán adquirir habilidades que les serán útiles en grados superiores, y que tienen muchas aplicaciones prácticas.

Construir Puntos Medios, Mediatrices y Bisectrices en Segmentos y ángulos

Puntos Medios de Segmentos Horizontales de Recta Mediatrices de Segmentos Horizontales de Recta Mediatrices de Segmentos de Recta Bisectrices de ángulos sin Rotar Bisectrices de ángulos Rotados

Construir Rectas Perpendiculares

Construir Líneas Perpendiculares a Través de Puntos sobre el Segmento Construir Líneas Perpendiculares a Través de Puntos fuera del Segmento Construir Líneas Perpendiculares a Través de Puntos sobre el Segmento (Con Rotación) Construir Líneas Perpendiculares a Través de Puntos fuera del Segmento (Con Rotación)

Hallar Centros de Triángulos

Hallar Baricentros en Acutángulos Hallar Ortocentros en Acutángulos Hallar Incentros en Acutángulos Hallar Circuncentros en Acutángulos Hallar Diferentes Centros en Acutángulos Hallar Baricentros en Acutángulos y Obtusángulos Hallar Ortocentros en Acutángulos y Obtusángulos Hallar Incentros en Acutángulos y Obtusángulos Hallar Circuncentros en Acutángulos y Obtusángulos Hallar Diferentes Centros en Acutángulos y Obtusángulos

Hojas de Ejercicios de Geometría en Tres Dimensiones

Los cubos conectados pueden ser una herramienta poderosa para desarrollar el sentido espacial de sus estudiantes. Las primeras dos hojas de ejercicios son difíciles incluso para los adultos, pero con un poco de práctica, sus estudiantes serán cacpaces de crear estructuras mucho más complejas que las que aparecen a continuación. Use papel cuadriculado isométrico y papel cuadriculado o puntuado para ayudar a sus alumnos a crear esbozos tridimensionales de cubos conectados y vistas laterales de estructuras.

Estructuras de Cubos

Vistas Laterales de Estructuras de Cubos Conectados Construir Estructuras de Cubos Conectados

Prismas y Pirámides

Clasificar Prismas Clasificar Pirámides Clasificar Prismas y Pirámides

Esta sección incluye una serie de desarrollos para que los estudiantes puedan construir los sólidos tridimensionales asociados. Se incluyen todos los sólidos platónicos y muchos de los arquimedianos. Sólo hacen falta unas tijeras, pegamento, y un poco de destreza manual. Para tener un resultado más resistente, pegue las impresiones o imprima directamente sobre cartulina. Revise que la impresora está configurada para imprimir en "Tamaño real" enlugar de ajustar el tamaño a la página, para que las proporciones sean las correctas.

Desarrollos de Sólidos

Desarrollo de Sólidos Platónicos y Arquimedianos Desarrollo de Todos los Sólidos Platónicos Desarrollo de Sólidos Arquimedianos Desarrollo de un Tetraedro Desarrollo de un Cubo Desarrollo de un Octaedro Desarrollo de un Dodecaedro (Versión 1) Desarrollo de un Dodecaedro (Versión 2) Desarrollo de un Icosaedro Desarrollo de un Tetraedro Truncado Desarrollo de un Cuboctaedro Desarrollo de un Cubo Truncado Desarrollo de un Octaedro Truncado Desarrollo de un Rombicuboctaedro Desarrollo de un Cuboctaedro Truncado Desarrollo de un Cubo Romo Desarrollo de un Icosidodecaedro Desarrollo de Sólidos Platónicos y Arquimedianos Desarrollo de Todos los Sólidos Platónicos Desarrollo de Sólidos Arquimedianos Desarrollo de un Tetraedro Desarrollo de un Cubo Desarrollo de un Octaedro Desarrollo de un Dodecaedro (Versión 1) Desarrollo de un Dodecaedro (Versión 2) Desarrollo de un Icosaedro Desarrollo de un Tetraedro Truncado Desarrollo de un Cuboctaedro Desarrollo de un Cubo Truncado Desarrollo de un Octaedro Truncado Desarrollo de un Rombicuboctaedro Desarrollo de un Cuboctaedro Truncado Desarrollo de un Cubo Romo Desarrollo de un Icosidodecaedro

Funciones Trigonométricas en Triángulos

Las funciones trigonométricas son muy útiles para determinar las dimensiones de un triángulo rectángulo. Las tres funciones básicas son seno, coseno y tangente. El seno se representa y calcula de la siguiente forma: sen(α) = C.O./H donde α es la medida del ángulo; C.O. se refiere a la longitud del (C)ateto (lado) (O)puesto al ángulo en cuestión, y H se refiere a la longitud de la (H)ipotenusa del triángulo rectángulo. El coseno por su parte se representa y calcula así: cos(α) = C.A./H donde C.A. se refiere al (C)ateto (A)dyacente al ángulo. La tangente se representa y calcula como sigue: tan(α) = C.O./C.A. Para mayor información, vean nuestra Guía de las funciones trigonométricas en triángulos rectángulos.

Funciones Trigonométricas en Triángulos

Calcular ángulos usando la Función Seno Calcular Lados usando la Función Seno Calcular ángulos y Lados usando la Función Seno Calcular ángulos usando la Función Coseno Calcular Lados usando la Función Coseno Calcular ángulos y Lados usando la Función Coseno Calcular ángulos usando la Función Tangente Calcular Lados usando la Función Tangente Calcular ángulos y Lados usando la Función Tangente Calcular ángulos usando Funciones Trigonométricas Calcular Lados usando Funciones Trigonométricas Calcular ángulos y Lados usando Funciones Trigonométricas